SEMANA 11

Para comenzar terminaremos el aprendizaje de las ecuaciones entre números Enteros, para esto daremos un repaso estudiaremos las diferentes formas en que se nos puede presentar una ecuación.

• ECUACIÓN DE LA FORMA      X ±  b =  C  

Como hemos visto un ejemplo de estas ecuaciones es:

• ECUACIÓN DE LA FORMA      ax = c

En estas ecuaciones ya no aparecen sumas y restas simplemente la variable esta multiplicada por un número entero, un ejemplo de estas ecuaciones es:

• ECUACIÓN DE LA FORMA   aX ±  b =  C 

En este tipo de ecuaciones la variable va multiplicada por un número entero seguido va una suma o resta, un ejemplo de estas ecuaciones es:

VÍDEO EXPLICATIVO:

Ecuaciones Entre Números Enteros Video Explicación 

INECUACIONES CON NÚMEROS ENTEROS

Una inecuación es una desigualdad algebraica en la que sus dos miembros aparecen ligados por uno de estos signos:

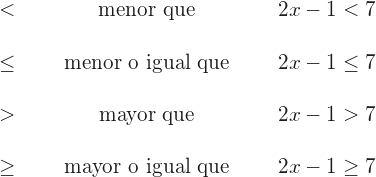
La solución de una inecuación son todos los puntos (números) que cumplen la desigualdad. La solución de una inecuación SIEMPRE va a ser un conjunto de puntos; es decir, un intervalo.

Para la solución de una inecuación se deben tener en cuenta las siguientes PROPIEDADES:

• Al sumar o restar la misma cantidad a los dos miembros de una inecuación la desigualdad no cambia.
• Al multiplicar o dividir los dos miembros de una inecuación por un mismo número positivo, la desigualdad no cambia.
• Al multiplicar o dividir los dos miembros de una inecuación por un mismo número Negativo, el sentido de la desigualdad cambia.

SEMANA 12

Teniendo en cuenta las diferentes formas de despejar una variable en una ecuación y con base a la  información anteriormente expuesta sobre las inecuaciones, a continuación se darán algunos ejemplos con cada una de las desigualdades, con el fin de entender mejor la forma de solución de estos ejercicios.

Tengamos en cuenta que la inecuación a diferencia de las ecuaciones NO se utiliza la igualdad (=), en las inecuaciones se usan los términos: 

• <        Menor que

• >       Mayor que

• ≤       Menor o igual que

• ≥       Mayor o igual que

EJEMPLOS:

• <        MENOR QUE:

• >        MAYOR QUE:

SEMANA 14

NÚMEROS RACIONALES

Los números racionales se aplican en diversas situaciones para representar la relación entre dos cantidades o magnitudes. Así, en física se utilizan números racionales para expresar la relación entre la distancia recorrida por un automóvil en un tiempo determinado; en economía se usan para indicar porcentajes, en química para medir  la concentración de una sustancia en un cuerpo, y en general, en cualquier área en la que se deba expresar una medida.

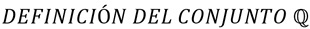
El conjunto de los números racionales se simboliza con la letra Q y se define como:

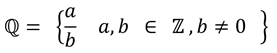
Por ejemplo, las fracciones 4/3  ;  - 2/5  y   8/9   son números racionales. De la misma forma, todo número entero es un número racional porque  se puede escribir como una fracción.

Así, el número 2 se puede escribir como: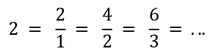  

FRACCIONES EQUIVALENTES

Dos fracciones son equivalentes cuando representan la misma parte de una unidad. Por ejemplo,  

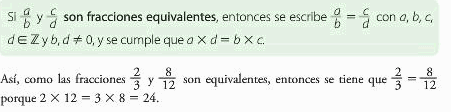
VÍDEO EXPLICATIVO

TERCER PERIODO

SEMANAS 17 Y 18

NÚMEROS RACIONALES

Siguiendo el desarrollo histórico de los números, se considera que, probablemente, fue la necesidad de lograr mayor precisión en las mediciones, un motivo muy importante para extender los sistemas numéricos hasta incluir otros números, además de los enteros. Estos son los llamados números racionales, a los que frecuentemente se les conoce como fracciones. Existen números racionales negativos, pero en principio, se estudiarán solamente los racionales positivos

Para comprender cómo se realiza la extensión del sistema numérico de los números naturales hasta los racionales, es necesario emplear modelos físicos (figuras geométricas regulares) que explican y permiten entender los conceptos de números racionales.

Se establece una unidad básica, que puede ser una figura geométrica regular; a continuación se divide en cierto número de partes iguales; esas partes, comparadas con la unidad, permiten crear un modelo de los números racionales. Ejemplo: un cuadrado se considera como unidad porque se divide en dos partes iguales.

Una vez adoptado este modelo, se requiere asociar un número con la parte sombreada del cuadrado, y un nombre para ese número. El nombre debe recordar las dos partes iguales que se tienen. Por lo tanto, de la relación de ambos números se obtiene un número racional.

Este es ½, y se lee "un medio".

En los ejemplos presentados, se ha sombreado una superficie menor que la unidad. Para comprender mejor el concepto de número racional, conviene observar otros modelos. En algunos casos, la parte sombreada cubre una superficie que es igual o mayor que la unidad. Como consecuencia, los números respectivos son iguales a 1, o mayores que 1.

Los números que tienen como modelos a estas figuras se llaman números racionales.

La forma numérica, en la que comúnmente se expresan, se llama fracción.

Observando los modelos, se aprecia que b es el denominador y siempre nombra la cantidad de partes iguales en que se ha dividido la unidad, en tanto que a es el numerador y hace referencia al número de partes que se utilizan. Una de las razones por las que el denominador nunca es cero es que no tendría sentido referirse a una unidad dividida en cero partes.

De acuerdo con lo anterior:

El concepto y la representación de un número racional tienen gran aplicación en diferentes cálculos que se realizan para resolver situaciones que se presentan todos los días.

SEMANAS 19 Y 20

NÚMEROS MIXTOS

Un número mixto es un racional que se expresa como la suma de un entero y una fracción. Por ejemplo,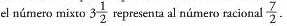  

En muchas ocasiones, la sola representación fraccionaria de una cantidad no nos da una idea de lo que poseemos.  Por ejemplo, si sabemos que tenemos 3/4 de pizza es fácil visualizar una pizza dividida en cuatro partes iguales, e imaginar que tenemos tres de ellas.  Sin embargo, si nos dicen que tenemos 19/7  ya no es tan fácil.  Estas situaciones se presentan cuando tenemos una fracción impropia.

Para ayudarnos a visualizar la fracción 19/7  hacemos lo siguiente: recuerda que un séptimo es una de las partes que se obtiene al dividir una unidad en siete partes iguales... ¿cuántos séptimos se necesitan para completar una unidad?  Precisamente siete, observa la siguiente imagen:

Para saber cual es la equivalencia de los números mixtos se siguen los siguientes pasos:

Conversión de fracción a número mixto:

Para convertir una impropia a número mixto se realizan los siguientes pasos:

Primero: Se divide el numerador entre el denominador.

Segundo: Se toma el cociente de la división como la parte entera del número mixto.

Tercero:  Se escribe la parte fraccionaria teniendo en cuenta que el numerador es el residuo de la división y el denominador es el divisor. 

EJEMPLOS:

solución

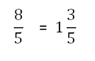
SEMANAS 21 Y 22

FRACCIONES DECIMALES

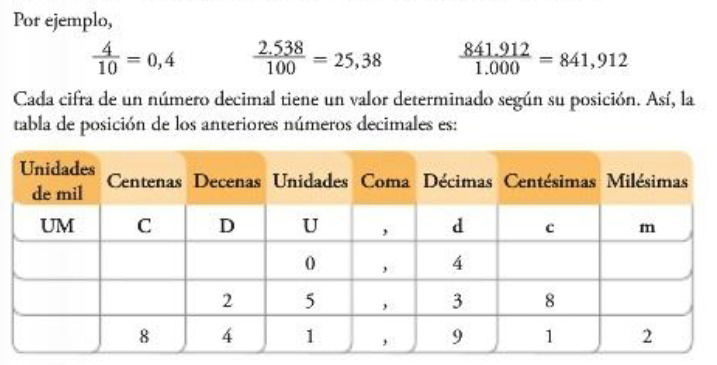
Una Fracción decimal es una fracción en la cual el denominador (el número de abajo) es una potencia de diez (como 10, 100, 1000, etc.).  Los números decimales son en si un tipo de número fraccionario. Por ejemplo el decimal 0.5 representa exactamente la fracción 5/10. La fracción 43/100 es también la representación de un decimal, es lo mismo entonces que 0.43. Veamos algunos otros ejemplos más claros: 

Una fracción decimal se puede representar mediante un número decimal. Los números decimales están formados por una parte entera, que se escribe antes de la coma y por una parte decimal  que se escribe después de la coma. Para expresar una fracción decimal con un número decimal se escribe el numerador y se separan de derecha a izquierda sus cifras con una coma, según la cantidad de ceros que tenga el denominador 

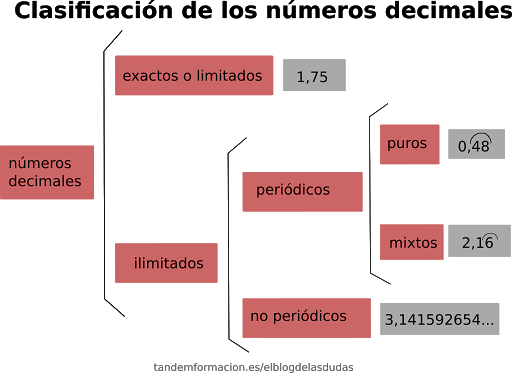
- Clasificación de los números racionales decimales.

Los números decimales se clasifican en números decimales exactos y números decimales periódicos, los cuales a su vez pueden ser periódicos puros o periódicos mixtos.

SEMANAS 23 Y 24

RACIONALES  DECIMALES

Ya sabemos que un número racional se puede expresar mediante una fracción, pero también se puede expresar mediante un número decimal 

Todo número racional en forma de fracción de enteros es una división desde el punto de vista numérico.

Así, si tomamos un número racional y hacemos la división entre su numerador y denominador, obtenemos la llamada expresión decimal del número racional.

Los números racionales pueden ser expresados como números que contienen decimales: 

Notación fraccionaria	Notación decimal
1/2	0,5
1/3	0,33
1/4	0,25
2/4	0,5
3/4	0,75
4/4	1

Los números decimales tiene una clasificación especifica a partir de las características que tenga su parte decimal.

Caso 1: Hacemos la división y obtenemos una expresión decimal exacta o finita como la de .

Se dice en este caso que el numero racional es decimal exacto o con expresión decimal finita, ya que su división en algún momento termina (su residuo es cero).

Caso 2: Si buscamos la expresión decimal de , observamos que la división no tiene fin y que siempre sale la misma cifra en la parte decimal ( esa parte que se repite no tiene porque ser una sola cifra como veremos más adelante), lo expresamos con la ayuda de puntos suspensivos

 y para abreviar se utiliza un semicírculo (gorrito) en la parte superior de la(s) cifra(s) que se repite o repiten como ves a continuación en nuestro ejemplo

En este caso decimos que el número racional es periódico puro.

Caso 3: Finalmente, puede ocurrir que al hacer la división nos encontremos que en la parte decimal del número haya una parte que no se repite y a continuación una o varias cifras que se repiten sin fin.

Este es el caso de

Si seguimos la misma notación que en el caso anterior escribimos  y se dice que el número racional es decimal periódico mixto, su periodo no se repite inmediatamente después de la coma.

ORDEN DE LOS RACIONALES Y DECIMALES

Los números racionales también representan cantidades, por lo tanto unos pueden representar más y otros menos, es decir, hay una relación de orden entre los mismos.  Debes entonces estar en la capacidad de poder determinar cuándo un número fraccionario o un número decimal es mayor que otro.

- NÚMEROS RACIONALES MENORES QUE 1

Todos los números racionales negativos son menores que 1 y los números  positivos que tengan el numerador menor  que el denominador,  ya que su división resulta ser un número decimal 

CUARTO  PERIODO

SEMANAS 28 Y 29

 RAZONES Y PROPORCIONES

En este nuevo apartado nos adentraremos en un nuevo tema llamado razones y proporciones, para ello veremos sus definiciones, algunos ejemplos y aplicaciones; comencemos.

Las razones y proporciones se aplican en diversas áreas como arte, arquitectura, cartografía, medicina, culinaria, entre otras. Por ejemplo, en cartografía se utilizan las razones para relacionar las dimensiones reales con las dimensiones del plano a mapa que las representa.

RAZÓN

Una razón es una comparación o cociente entre dos cantidades a y b con b diferente de cero, este cociente entre estas cantidades se simboliza 

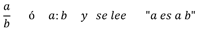
En la razón anterior  a es el antecedente y  b es el consecuente 

Una razón puede presentar la relación entre dos cantidades de una misma magnitud o la relación entre dos cantidades de diferentes magnitudes. En este ultimo caso, la razón tiene una unidad de medida.

Por ejemplo, si se establece la razón d/t  con t diferente de cero, en donde d representa la distancia recorrida por un automóvil en un tiempo t, entonces la unidad de medida puede ser kilómetros por hora, metros por segundo, entre otros.

EJEMPLO:

1. Escribir la expresión 5 es a 18 como una razón. Luego, identificar el antecedente y el consecuente.

Rta/

la razón correspondiente se puede escribir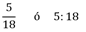  

en esta razón 5 es el antecedente y 8 es el consecuente.

2.  

SERIE DE RAZONES IGUALES

Una serie de razones iguales es la igualdad entre dos o mas razones:

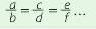
SEMANAS 30 Y 31

PROPORCION