SEMANA 11

Complementando la información investigada en el cuarto corte del primer periodo veremos:

POLINOMIOS

POLINOMIO

Un polinomio es una expresión algebraica formada por sumas o restas de dos o más monomios. Los monomios que conforman el polinomio se denominan términos del polinomio.

En particular a un polinomio conformado por dos monomios se le denomina binomio y a un polinomio que consta de tres términos se le denomina trinomio.

EJEMPLOS:

• m n²   +  3m² n               consta de dos términos (Binomio)

• 7ab²  - 7b + 4                  consta de tres términos (Trinomio)

• 2x + 4yx - x - 28y + 9      consta de 5 términos (polinomio)

CARACTERÍSTICAS DE UN POLINOMIO

1. GRADO ABSOLUTO DE UN POLINOMIO

El grado absoluto de un polinomio es el mayor grado de los términos del polinomio. 

Por ejemplo, en el binomio a² b - ab , el grado de a² b es 3 pues se suma el exponente 2 de a y 1 de b y el de ab es 2 ya que se suma el exponente 1 de a y 1 de b; es por esto que el grado absoluto del polinomio es 3 pues es el grado mayor de todos los términos.

   2. GRADO RELATIVO DE UN POLINOMIO

El grado relativo de un polinomio se toma con respecto a una variable, para ello se toma el mayor exponente de la variable escogida.

Por ejemplo, 2x² y + 3xy³ , si tomamos como referencia a x el mayor exponente es 2 y si tomamos como referencia a y su mayor exponente es 3; por tanto el grado absoluto del polinomio con respecto a x es 2 y con respecto a y es 3.

  3.  TERMINO INDEPENDIENTE  

El termino independiente de un polinomio es el termino de grado cero en el polinomio; es decir, la constante o el número que no va acompañado por ninguna variable.

Por ejemplo, en el polinomio 7y⁴ + 5y³ + 12, el termino independiente es 12 porque su grado es cero, es decir 12y⁰ = 12.

  4.  TÉRMINOS SEMEJANTES

Dos o más términos de un polinomio son semejantes cuando su parte literal es la misma, es decir, cuando las variables de ambos términos con sus respectivos exponentes, son exactamente iguales.

Por ejemplo, los términos -5x²y z³  y  7yx²z³   son semejantes porque sus variables con sus respectivos exponentes son los mismos.

SEMANA 12

En esta sección se exponen dos vídeos acerca del lenguaje algebraico, términos, monomio y polinomios; con el fin de esclarecer las dudas que aun se presenten y poder avanzar en la siguiente sección.

Se recomienda ver detalladamente los vídeos comparando la información con la solución de la actividad que realizo en la semana 11.

SEMANA 13

SUMA Y RESTA DE MONOMIOS

SUMA

Para sumar  dos o mas monomios se requiere que estos sean semejantes. Para ello, se suman o se restan los respectivos coeficientes de cada monomio y a continuación se escribe la misma parte literal. A este proceso se le denomina reducción de términos semejantes.

Ejemplo:

• 3x⁴ y³      y       7x⁴ y³

PRIMERO: se verifica que los dos monomios sean semejantes para poder reducir los términos mediante la suma.

SEGUNDO: Se suman los coeficientes de cada monomio y la parte literal se deja igual,  así:

3x⁴ y³   +    7x⁴ y³   =  (3 + 7) x⁴ y³   =  10 x⁴ y³  

• 2m³ n⁴ +  6m³ n⁴  =    (2+6)m³ n⁴     =  8m³ n⁴   

• Sumar     3m³ n²    ;    -4m³ n²      ;   -5m³ n²  

PRIMERO: se verifica que los dos monomios sean semejantes para poder reducir los términos mediante la suma.

SEGUNDO: Se suman los coeficientes de cada monomio teniendo en cuenta su signo y la parte literal se deja igual,  así:

RESTA

La resta entre monomios sigue el mismo procedimiento que en la suma, se verifica que los monomios sean semejantes, posteriormente se realiza la resta de los coeficientes y se deja igual la parte literal.

EJEMPLOS:

• De  5r⁴ y²  restar  2r⁴ y² 

• De   -7u⁸ v⁷  de  9u⁸ v⁷

SEMANA 14

SUMA Y RESTA DE POLINOMIOS

Para determinar las operaciones aditivas entre polinomios se realiza lo que se indica a continuación.

• Para sumar dos polinomios:  Primero, se escriben los polinomios planteando la suma y luego se reducen los términos semejantes de los polinomios dados; cuando hablamos de reducir nos referimos a realizar la suma de los coeficientes de los términos que sean semejantes.

• Para restar dos polinomios:  Primero, se escriben los polinomios planteando la resta y luego se reducen los términos semejantes de los polinomios dados; cuando hablamos de reducir nos referimos a realizar la resta de los coeficientes de los términos que sean semejantes  teniendo en cuenta la ley delos signos.

VÍDEO EXPLICATIVO

TERCER PERIODO

SEMANAS 17 Y 18

MULTIPLICACIÓN DE MONOMIOS Y POLINOMIOS

EJEMPLOS

SEMANAS 19 Y 20

DIVISIÓN ENTRE MONOMIOS 

1.1. DIVISIÓN DE MONOMIOS

El  cociente o división entre dos monomios es otro monomio cuyo coeficiente es el cociente de los coeficientes, y la parte literal es el cociente de la partes literales aplicando la división de potencias de igual base.

1.2. DIVISIÓN DE UN POLINOMIO ENTRE UN MONOMIO

Para dividir un polinomio entre un monomio, se divide cada uno de los términos del polinomio entre el monomio respectivo. Luego, se siguen las reglas de división entre monomios. 

SEMANAS 21 Y 22

DIVISIÓN ENTRE POLINOMIOS 

1.3. DIVISIÓN DE POLINOMIOS

Para dividir dos polinomios se puede utilizar el método habitual (para todo tipo de divisores) y la división sintética o regla de Ruffini (para divisores de la forma x+a  o de la forma x-a).

MÉTODO HABITUAL 

 Primero: Se ordenan los polinomios en forma descendente con respecto a una de las variables en caso que las potencias al descender falte un número se deja el espacio correspondiente al orden de las mismas .

Segundo:  Se divide el primer término del dividendo entre el primer término del divisor.  El resultado sera el primer término del cociente.

Tercero: Dicho término se multiplica por cada uno de los términos del divisor. Cada producto se resta de su semejante en el dividendo y se tienen en cuenta los respectivos cambios de signo. Si alguno de estos productos no tienen termino semejante en el dividendo, se escribe en el espacio que se dejo correspondiente al orden de las potencias.

Cuatro: Se baja  el siguiente término del dividendo. Se divide el primer término parcial entre el primer término del divisor. El resultado sera el segundo término del cociente.

Quinto: Se continua el proceso hasta que el residuo tenga un grado menor que el grado del divisor.

SEMANAS 23 Y 24

PRODUCTOS NOTABLES

1.1 CUADRADO DE UN BINOMIO

Cuando se halla el cuadrado de un binomio se deben tener en cuenta dos casos: el cuadrado de la suma de dos términos y el cuadrado de la diferencia o resta de dos términos.

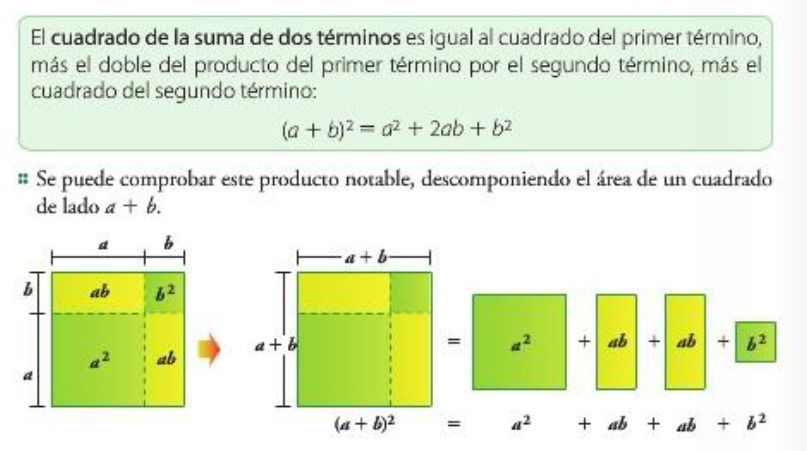
Los pasos a seguir parasolucionar el cuadradode un binomio son:

1. Escribiremos el cuadrado del primer término.
2. Sumaremos el doble del primero por el segundo término.
3. Sumaremos el cuadrado del segundo término.

EJEMPLOS:

Si aplicamos estas reglas a los ejemplos , tendremos:

a)     (x+z)²

1. Escribiremos el cuadrado del primer término: x²
2. Sumaremos el doble del primero por el segundo término: 2xz
3. Sumaremos el cuadrado del segundo término: z².

El resultado es: (x+z)²   =    x²  +  2xz  +  z²

b)   ( x + 4) ²

    ( x + 4) ²   =  x ²  +  2 ( x · 4)  + 4 ²

     = x ² + 8 x + 16

1.2. CUADRADO DE LA RESTA DE UN BINOMIO

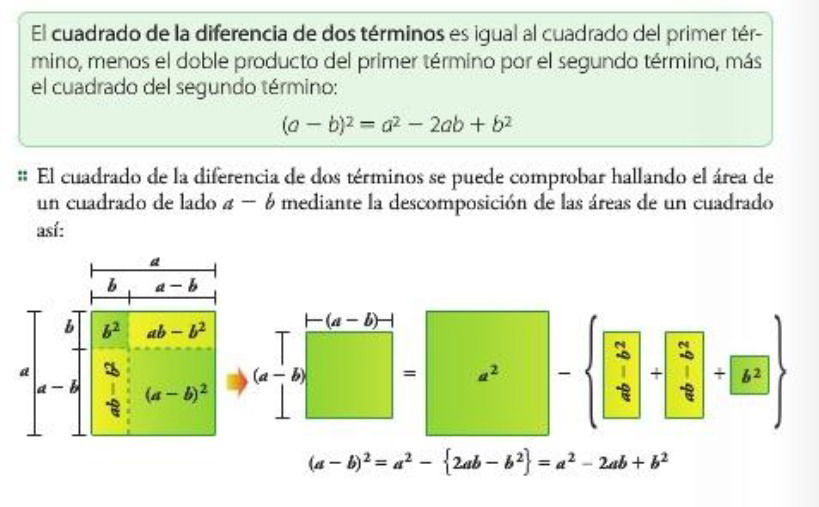
EJEMPLOS:

Si aplicamos estas reglas a los ejemplos , tendremos:

a)     (3m - y)²

1. Escribiremos el cuadrado del primer término: (3m)²  = 9m²
2. Restaremos el doble del primero por el segundo término: 2 (3m) (y) = 6my
3. Sumaremos el cuadrado del segundo término: y².

El resultado es: (3m - y)²  =    9m²  +  6my  +  y²

b) (3 p - 2 q ² )

    (3 p - 2 q ² )  =  (3 p ) ² - 2 (3 p · 2 q ² ) + (2 q ² ) ²

         = 9 p ² - 2 (6 pq ² ) + 4 q ⁴

         = 9 p ² - 12 pq ² + 4 q ⁴

CUARTO  PERIODO

SEMANAS 28 Y 29

 Cuadrado de un trinomio

El cuadrado de un trinomio puede relacionarse con el cálculo del área de un cuadrado cuyo lado mida a+b+c , mediante la propiedad distributiva o aplicando el producto notable del producto del cuadrado  de un binomio.

Esta igualdad la podemos demostrar de las siguientes formas: 

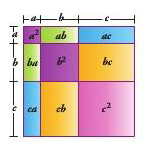
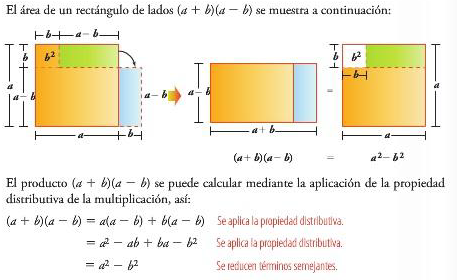
PRODUCTO DE LA SUMA POR LA DIFERENCIA

La suma por la diferencia de dos términos se puede demostrar como el área de un rectángulo cuyas medidas de los lados son a+b   y   a-b  o multiplicando los términos y aplicando la propiedad distributiva. 

SEMANAS 30 Y 31

CUBO DE UN BINOMIO

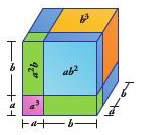
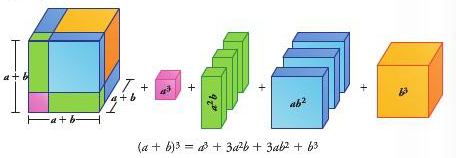
EJEMPLO:

• (4 + 2x)³  

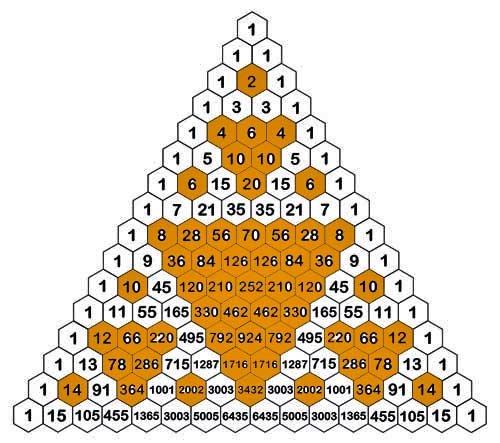
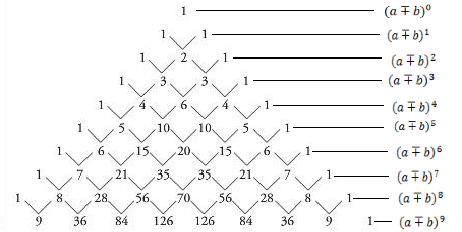
EL TRIÁNGULO DE PASCAL

El triángulo de Pascal es un arreglo de números que permite hallar los coeficientes de expresiones de la forma :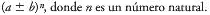 

El triángulo de Tartaglia también se conoce como triángulo de Pascal ( se de nomina de esta forma en honor a Blaise Pascal, matemático, físico, filósofo y teólogo francés) en las ciencias matemáticas el triángulo de Pascal es un conjunto infinito de números enteros que se encuentran ordenados en forma triangular, allí están expresados los coeficientes binomiales.

Para empezar, debemos armar el triángulo de la siguiente manera. Se comienza con un número uno hasta arriba de la pirámide, luego se colocan otros dos unos debajo del primero de forma triangular. Ahora, se comienzan a sumar de dos en dos los números, anotando el resultado debajo de ellos, y así consecutivamente con el resto de los números. Todos los números son el resultado de la suma de los dos de arriba y lo extremos siempre van a ser uno.

Pares, impares y un tal Sierpinski.

 Waclaw Sierpinski (1882-1969) fue un matemático polaco que en 1919 creo el llamado “triángulo de Sierpinski” que entre otras cosas, demostraba que era posible hacer una curva que se cruzara consigo misma en todos sus puntos. El triángulo es un fractal, un fractal es un objeto cuya estructura básica de repite en diferentes escalas. Lo curioso de este triángulo, es que tiene una relación muy interesante con el triángulo de Pascal. Si al triangulo de Pascal le hacemos una modificación coloreando todos los números pares de un color y los impares de otro conseguiremos un triángulo muy parecido al del señor Sierpinski.