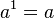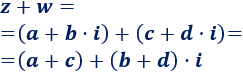MATEMÁTICAS - NOVENO
SEMANA 11
POTENCIACIÓN Y RACIONALIZACIÓN
En este apartado haremos un pequeño repaso al concepto de potenciación y racionalización de números Reales.
POTENCIACIÓN
La potenciación permite expresar números muy grandes como la distancia del sol a la tierra o muy pequeñas como la carga eléctrica de un electrón. Además, con la potenciación se puede formular expresiones que permitan modelar fenómenos en biología, química, física, entre otras áreas. Por ejemplo, las leyes de Kepler, que describen los movimientos de los planetas en sus órbitas alrededor del sol, se plantea a partir de expresiones que incluyen potencias al cuadrado y al cubo.
DEFINICIÓN: La POTENCIACIÓN es la operación que permite expresar, en forma simplificada, la multiplicación de varios factores.
En la potenciación de números reales el exponente puede ser entero positivo, entero negativo o cero.
Ejemplos:
- La multiplicación -7 * -7 = 49 se puede expresar como (-7)2 = 49. En este caso, -7 es la base , 2 es el exponente y 49 es la potencia.
- Hallar la potencia:
(-12)3 = (-12) * (-12) * (-12)
= (+144) * (-12)
= 1.728
En la potenciación se deben tener en cuenta algunas propiedades como son:
PROPIEDADES DE LA POTENCIACIÓN:
- Potencia de exponente cero
Toda potencia de exponente 0 y base distinta de 0 es igual a 1.
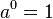 si se cumple que
si se cumple que 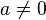
- Potencia de exponente 1
Toda potencia de exponente 1 es igual a la base
ejemplo:
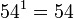
- Producto de potencias de igual base
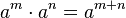
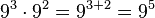
- División de potencias de igual base
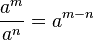
- Potencia de un producto
- Potencia de una división
- Potencia de una potencia
- Potencia de exponente negativo
- Potencia de exponente fraccionario
El producto de dos o más potencias de igual base (a) es iguala la potencia de base a y exponente igual a la suma de los correspondientes exponentes. Se coloca la misma base y se suman los exponentes.
ejemplos:
La división de dos potencias de igual base (a) es igual a la potencia de base a y exponente igual a la resta de los exponentes respectivos. Se coloca la misma base y se restan los exponentes.
La potencia de un producto de base (a*b) y de exponente "n" es igual a la potencia "a" a la "n" por "b" a la "n". Cada base obtiene el exponente
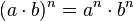
En la potencia de una división de base "a/b" y exponente "n" se procede a elevar cada uno de los componentes de la base a "n".
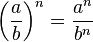
La potencia de una potencia de base a es igual a la potencia de base a elevada a la multiplicación de ambos exponentes. Se coloca la misma base y se multiplican los exponentes
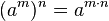
Una potencia que tenga exponente negativo se cambia de lugar en una fracción y de este modo su exponente sera positivo.
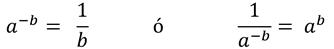
Es una potencia que tiene su exponente en forma de fracción, y en la que se cumple que
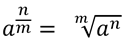
SEMANA 12
En esta sección se exponen dos vídeos acerca del termino potencia y las propiedades de la potencia; con el fin de esclarecer las dudas que aun se presenten y poder avanzar en la siguiente sección.
Se recomienda ver detalladamente los vídeos comparando la información con la solución de la actividad que realizo en la semana 11.
SEMANA 13
RACIONALIZACIÓN
Para entender la racionalización primero debemos saber que es un radical.
RADICAL:
La raíz enésima de un número real a es un número real b, si y sólo si la enésima potencia de b es a. Es decir,
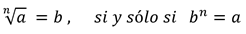
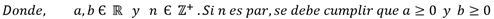
Cuando en una raíz no se indica el indice significa que dicho indice es 2, y por tanto corresponde a la raíz cuadrada.
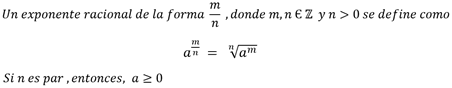
- En la radicación al igual que en la potenciación se deben tener en cuenta algunas propiedades:

- Ejemplo
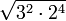 =
= 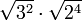 =
= 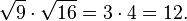
Se llega a igual resultado de la siguiente manera:
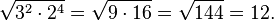
SEMANA 14
RACIONALIZACIÓN
Cuando un radical se simplifica en su forma mas simple, también se debe tener en cuenta que en el denominador no haya radicales y que ninguna fracción debe aparecer dentro de un radical.
Racionalizar una expresión fraccionaria en la que el denominador contiene uno o varios radicales consiste en expresarla como una fracción equivalente sin radicales en el denominador.
En la racionalización de fracciones se distinguen dos casos: cuando los denominadores son monomios y cuando los denominadores son binomios.
RACIONALIZACIÓN DE FRACCIONES CON DENOMINADORES MONOMIOS.
Para racionalizar el denominador, se multiplican el numerador y el denominador por un radical, es decir, se complifica la fracción de tal forma que el radical del denominador tenga raíz exacta.
EJEMPLO:
1. 
2. 
RACIONALIZACIÓN DE FRACCIONES CON DENOMINADORES BINOMIOS.
Para racionalizar un denominador compuesto por dos términos, en una fracción se tienen en cuenta dos casos:
- Si el denominador es un binomio que contiene radicales de indice dos, se debe multiplicar la fracción por el mismo binomio pero con el signo opuesto al segundo término. Esta expresión recibe el nombre de conjugado.
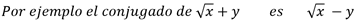
- Si el denominador es un binomio que contiene radicales de índice tres, entonces la fracción se debe multiplicar por el trinomio que convierte el producto del denominador en una suma o diferencia de cubos.

TERCER PERIODO
SEMANAS 17 Y 18
NÚMEROS COMPLEJOS
Para lograr entender los números complejos iniciaremos estudiando los números imaginarios.
1. NÚMEROS IMAGINARIOS
Los números imaginarios tienen variadas aplicaciones en diferentes campos. En electrónica para procesar, restaurar y optimizar señales; en la teoría de control (área que relaciona la ingeniería y la matemática); en física donde están relacionados con electromagnetismo, el análisis de vibraciones y otras áreas.
Las ecuaciones de la forma x2 + a = 0, donde a es un número real positivo, no tienen solución en el conjunto numérico de los números reales porque el cuadrado de un número real es un número no negativo y al ser sumado con un número positivo su resultado no es cero.
Para dar solución a este tipo de ecuaciones, se generó un nuevo conjunto numérico denominado números imaginarios.
La unidad principal o unidad imaginaria se representa con la letra i y cumple las siguientes propiedades :

1.1 Números imaginarios puros
Los números que se expresan como el producto de un número real, diferente de de cero, por la unidad imaginaria reciben el nombre de imaginarios puros.
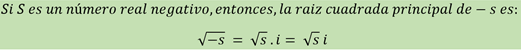

1.2 Potencias de i
Las potencias de la unidad imaginaria i se obtienen aplicando las propiedades de la potenciación y la definición de i, i2 , como sigue:
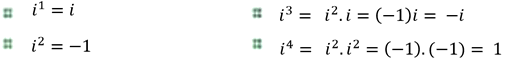
Estas cuatro potencias de i se denominan potencias básicas de i , ya que a partir de de i5 se repiten en periodos de cuatro. Así, i5 = i4 . i = 1 .i = i

SEMANAS 19 Y 20
NÚMEROS COMPLEJOS
| Definición |
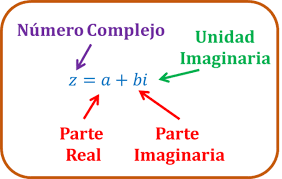
Un número complejo tiene la forma a+ b i donde a y b son números reales: a se conoce como la parte real y b se conoce como la parte imaginaria. |

REPRESENTACIÓN GRÁFICA DE LOS NÚMEROS COMPLEJOS
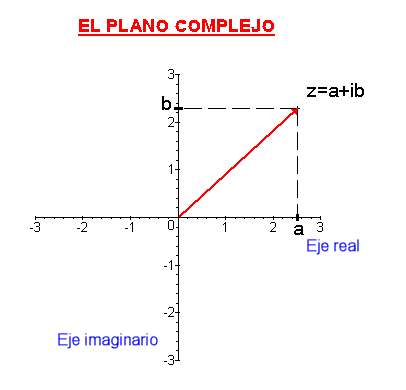
Todo número complejo se puede representar geométricamente sobre el plano complejo. El plano complejo es un sistema de coordenadas rectangulares, en el cual el eje horizontal es el eje real y el eje vertical es el eje imaginario.
Así, para representar el número a + bi se usa su forma cartesiana (a,b) donde la primera componente a se ubica sobre el eje real y la segunda componente b se ubica sobre el eje imaginario.
SEMANAS 21 Y 22
OPERACIONES CON NÚMEROS COMPLEJOS
1.1. ADICIÓN DE NÚMEROS COMPLEJOS
Para sumar dos o mas números complejos se suman, respectivamente, las partes reales y las partes imaginarias; es decir:
Ejemplo Sumar (4+5i) y (4+6i)
Solución
(4+5i)+(4+6i)=(4+4)+(5+6)i
=8+11i
1.2 RESTA DE NÚMEROS COMPLEJOS
Para restar dos o más números complejos se restan, respectivamente, las partes reales y las partes imaginarias.
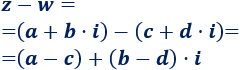
Ejemplo Realice la resta (3−2i)−(4+6i).
Solución
(3−2i)−(4+6i)==(3−4)+(−2−6)i−1−8i
1.3 MULTIPLICACIÓN DE NÚMEROS COMPLEJOS.
Para multiplicar dos números complejos se realizan los siguientes pasos:
Primero: Se aplica la propiedad distributiva.
Segundo: Se resuelven las operaciones entre términos semejantes.
Finalmente: Se resuelven las potencias de i, se reducen términos semejantes.
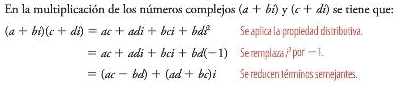
EJEMPLOS:
A.
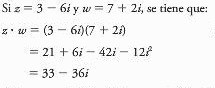
B. Si z= 1-i y w=2- 3i
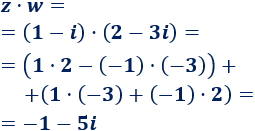
SEMANAS 23 Y 24
DIVISIÓN DE NÚMEROS COMPLEJOS
Una división de complejos se expresa así:
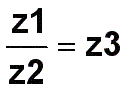 |
| Estos es: | 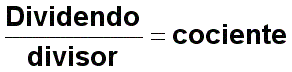 |



EJEMPLO RESUMIDO:
Para dividir números complejos en forma binómica se multiplica numerador y denominador por el conjugado del denominador y se realizan las operaciones correspondientes.
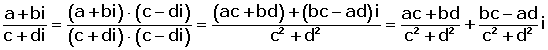
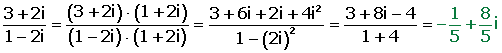
CUARTO PERIODO
SEMANAS 28 Y 29
SISTEMAS DE ECUACIONES LINEALES
Un sistema de ecuaciones lineales es un conjunto formado por dos o más ecuaciones lineales, cada una de ellas con dos o más incógnitas.
Existen diferentes tipos de sistemas de ecuaciones dependiendo del número de variables y ecuaciones que se tengan en el conjunto, por ejemplo:

Los sistemas de ecuaciones nacen de situaciones en las que no es muy claro las operaciones a realizar para encontrar los valores desconocidos .

Métodos para la solución de sistemas de ecuaciones lineales
Para la solución de un sistema de ecuaciones lineales se pueden usar diferentes métodos, por lo que esta unidad esta dedicada a estudiar los métodos mas importantes y utilizados.
MÉTODO DE SUSTITUCIÓN
Para resolver un sistema de ecuaciones lineales por el método de sustitución, se realizan los siguientes pasos:
- Primero: Se despeja una de las variables en cualquiera de las ecuaciones dadas.
- Segundo: Se reemplaza la expresión obtenida en el primer paso en la otra ecuación y se resuelve.
- Tercero: Se encuentra el valor de la otra variable reemplazando, en cualquiera de las ecuaciones del sistema, el valor de la variable hallado en el segundo paso.
- Cuarto: Se verifican las soluciones.
Ejemplo:
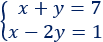
1. Despejamos la x en la primera ecuación:
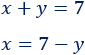
2. Ahora, sustituimos la expresión algebraica en la segunda, es decir, escribimos 7−y donde aparece x:
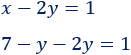
Resolvemos la ecuación:
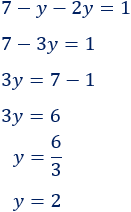
3. Como ya conocemos y, podemos calcular x a partir de la ecuación que obtuvimos al despejar x:
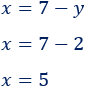
Por tanto, la solución del sistema es x=5 e y=2:
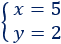
MÉTODO DE IGUALACIÓN
Para resolver un sistema de ecuaciones lineales por el método de igualación, se realizan los siguientes pasos:
- Primero: Se despeja la misma variable en las dos ecuaciones dadas.
- Segundo: Se igualan las expresiones obtenidas en el primer paso y se despeja la variable que queda.
- Tercero: Se determina el valor de la otra variable reemplazando en cualquiera de las ecuaciones despejadas, el valor de la variable hallado en el segundo paso.
- Cuarto: Se verifican las soluciones.
Ejemplo:
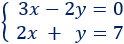
1. Despejamos la x en la primera ecuación:
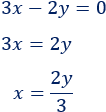
Despejamos la x en la segunda ecuación:
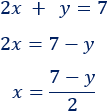
2. Igualamos las dos expresiones:
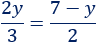
Resolvemos la ecuación obtenida:
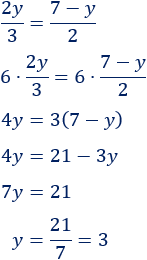
3. Como conocemos y, podemos calcular x (sustituyendo):
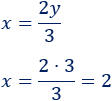
Por tanto, la solución del sistema es
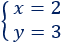
SEMANAS 30 Y 31
MÉTODO DE REDUCCIÓN
Para solucionar un sistema de ecuaciones 2x2 por este método se deben combinar las ecuaciones del sistema con el fin de reducir las dos ecuaciones del sistema a una sola, realizando los siguientes pasos:
- Primero: Se multiplican los términos de una o ambas ecuaciones por números reales, de tal manera que los coeficientes de una de las variables en las dos ecuaciones sea el mismo pero con diferente signo.
- Segundo: Se suman las ecuaciones transformadas de tal manera que se elimina una variable y se despeja la otra variable.
- Tercero: Se calcula el valor de la incógnita que falta sustituyendo en una de las ecuaciones originales
Cuando se resuelve se resuelve un sistema de ecuaciones lineales por el método de reducción se pueden presentar los siguientes casos:
- Caso 1 : Si al sumar las dos ecuaciones para eliminar una variable, se eliminan las dos variables, es decir, aparece la ecuación 0=c , donde c es una constante diferente de 0, el sistema no tiene solución, es decir es inconsistente.
- Caso 2 : Si al sumar las dos ecuaciones resulta la expresión 0=0 , el sistema tiene infinitas soluciones, es decir, dependiente o indeterminado.
- Caso 3: Si al sumar las ecuaciones se obtiene una expresión de la forma x=a, con a un número real, el sistema tiene una solución.


MÉTODO POR DETERMINANTES