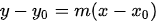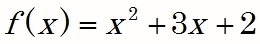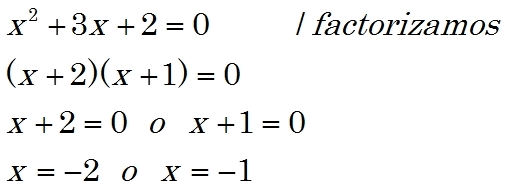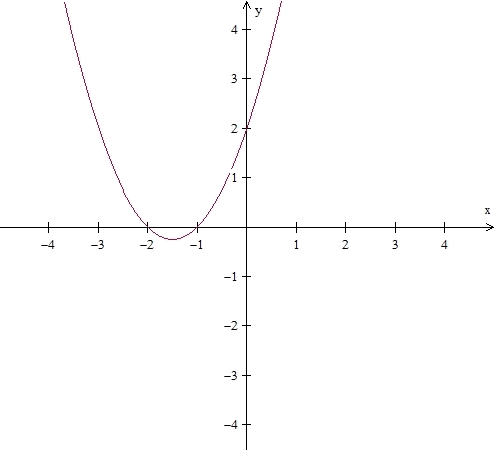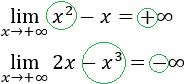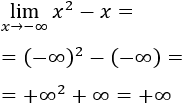SEMANA 11

GEOMETRÍA ANALÍTICA 

Iniciemos con algunos conceptos importantes.

LUGAR GEOMÉTRICO

Un lugar geométrico es un conjunto de puntos del plano cartesiano que cumplen con una característica geométrica común. 

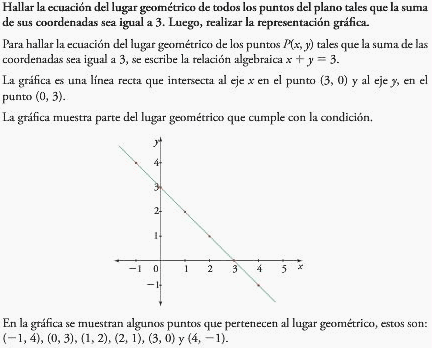
En relación con la característica común de los puntos que pertenecen al lugar geométrico del plano es posible realizar su representación analítica por medio de una ecuación, la cual se denomina ecuación del lugar geométrico. También es posible realizar la representación geométrica por medio de una gráfica en el plano cartesiano. 

Por ejemplo

• Considere el lugar geométrico representado por cualquier función, la grafica de la función representa la condición que existe entre los dos componetes (x y  y) mediante la condición que da la función, Así, el lugar geometrico de una función lineal   f(x) = ax + b  es la linea recta que se genera con los puntos (x , f(x) ). 
•  

RECTA

Existen ciertas definiciones de recta que aunque suenen distinto siempre se enfocan a lo mismo, pero para nuestro caso tomaremos como definición de la recta lo siguiente: " la recta es el lugar geométrico de los puntos tales que, tomados dos cualesquiera del lugar geométrico, el valor de la pendiente siempre resulta ser constante”. 

• Pendiente de la recta

Si P (X₁ , Y₁) y  Q(X₂ , Y₂)  son dos puntos sobre una recta L, entonces la pendiente de L denotada por "m" se define como: 

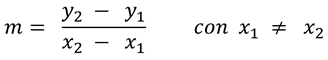
Tener en cuenta:

1. Cuando  la pendiente es negativa, la recta está inclinada hacia la izquierda.
2. Cuando la pendiente es positiva, la recta se inclina hacia la derecha.
3. En el  caso en que  m= 0, la recta se encuentra en posición horizontal. 

Por ejemplo, 

Encuentra la pendiente que pasa por los puntos A(-6, -4) y B(8 , 3)

Aplicando la formula:

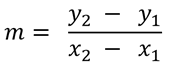
Se reemplazan las coordenadas de A  y   B

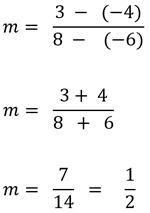
• Ecuación de la recta

Una recta puede ser expresada mediante una ecuación del tipo y = m x + b, donde x, y son variables en un plano. En dicha expresión m es denominada pendiente de la recta y está relacionada con la inclinación que toma la recta respecto a un par de ejes que definen el Plano. Mientras que b es el término independiente y es el valor del punto en el cual la recta corta al eje vertical en el plano. 

Ecuación fundamenta de la recta ó  Ecuación punto pendiente.

Dada una recta mediante un punto, 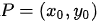, y una pendiente   m  :

Se puede obtener la ecuación de la recta a partir de la fórmula de la pendiente (ecuación punto-pendiente):

Ejemplo 

La ecuación de la recta que pasa por el punto 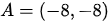y que tiene una pendiente de  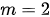es:

Sustituyendo en la ecuación anterior tenemos:

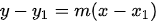
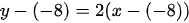
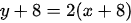
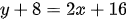
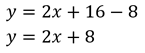
Ecuación  de la recta que pasa por dos puntos

Siendo P (X₁ , Y₁) y  Q(X₂ , Y₂) se puede obtener la ecuacion de la recta a partir de la siguiente ecuación y despejando y.

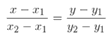
Ejemplo:

Hallar la ecuación de la recta que pasa por los puntos A(1, 3)  y  B(2, -5)

Sustituyendo en la anterior ecuación

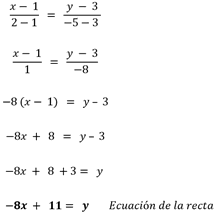
SEMANA 12

FUNCIÓN LINEAL

Una función de variable real se llama función lineal si tiene la forma

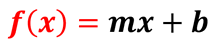
donde m y b son números reales constantes.

Elementos de la función lineal

En la función lineal, que siempre tiene la forma y = mx + b ; tenemos los siguientes elementos:

• x: variable independiente.
• y: variable dependiente (su valor depende del valor de x).
• m: pendiente.
• b: corte con el eje y, u ordenada de origen.

Características de la función lineal

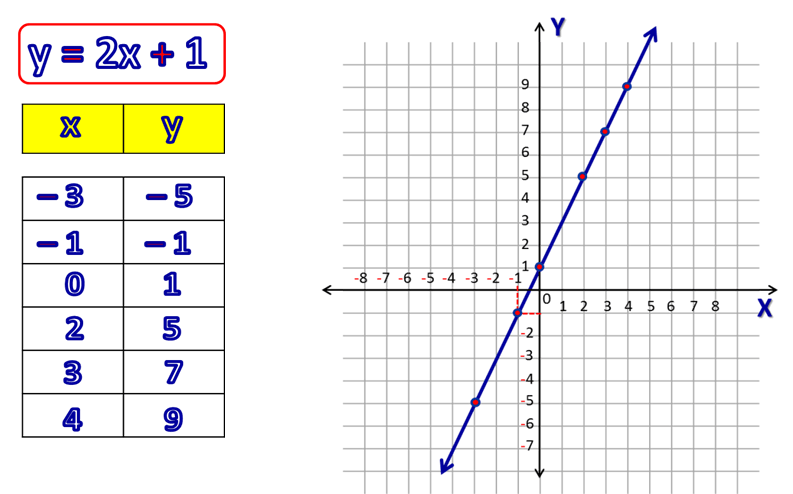
•  La gráfica de una función lineal es una recta en el plano cartesiano.
• si m  tiene un valor positivo,  la función lineal es una función creciente; es decir, si el valor de x  aumenta el valor de y   también va aumentando.
• si m  es un número real negativo, la función lineal es una función decreciente; es decir si el valor de x aumenta el valor de y disminuye o viceversa.

Veamos algunos vídeos para entender mejor el concepto de función lineal y como se gráfica:

• Primero veremos como se gráfica una función lineal haciendo uso de la tabla de valores

• Ahora veamos como se gráfica una función lineal sin tabla de valores.

SEMANA 13

FUNCIÓN CUADRÁTICA

Una ecuación de variable real se llama función cuadrática cuando se tiene una función polinomica de segundo grado y si tiene la forma 

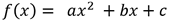
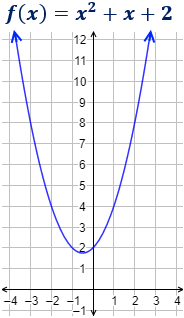
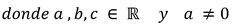 La gráfica de una función cuadrática siempre es una parábola.

EJEMPLO:

Se debe tener en cuenta que: 

• Cuando a >  0  la gráfica es una parábola que abre hacia arriba.      
  .
• Cuando a <  0  la gráfica es una parábola que abre hacia abajo.
• Cuando  el valor absoluto de a (|a|)  es grande la función crece mas rápido por lo que la parábola es mas cerrada;  contrario cuando a es pequeño la parábola es mas abierta pues crece mas lento.
• El valor de c  me define el punto de intersección de la  gráfica con el  eje y.

Para hallar el punto que me define el vértice de la parábola se usa la siguiente ecuación Para hallar el vertice de la parabola:

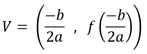
SEMANA 14

Retomando el estudio de la función cuadrática considerando las intersecciones con los ejes.

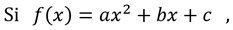
la gráfica de f intercepta (corta) al eje y en   y = c.  Para obtener las intersecciones con el eje X se debe resolver la ecuación:

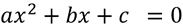
Existe dos formas de solucionar esta ecuación:

• Realizando la factorización de la forma de un trinomio de la forma ax² + bx + c  ; en donde se obtendrán dos términos que debemos iguala cero para obtener los valores de x.
• En caso que no se pueda realizar la factorización, se debe usar la ecuación cuadrática la cual nos dice que:

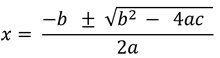
En donde llamaremos a b²  -4ac   el discriminante de la función cuadrática. Este discriminante tiene las siguientes características:

• Si   b²  -4ac  >  0    ,  la ecuación tiene  dos soluciones reales distintas.
• Si   b²  -4ac  <  0    ,  la  ecuación no tiene soluciones en los reales y la gráfica carece de intercepciones con el eje x.
• Si   b²  -4ac  =  0    ,  la ecuación tiene una única solución.

EJEMPLOS:

1  .           

Tendremos que, para calcular los puntos de corte de la parábola con el eje X debemos resolver la siguiente ecuación:

y su gráfica sería:

2.    

VÍDEO EXPLICATIVO

TERCER PERIODO

SEMANAS 17 Y 18

LA CIRCUNFERENCIA

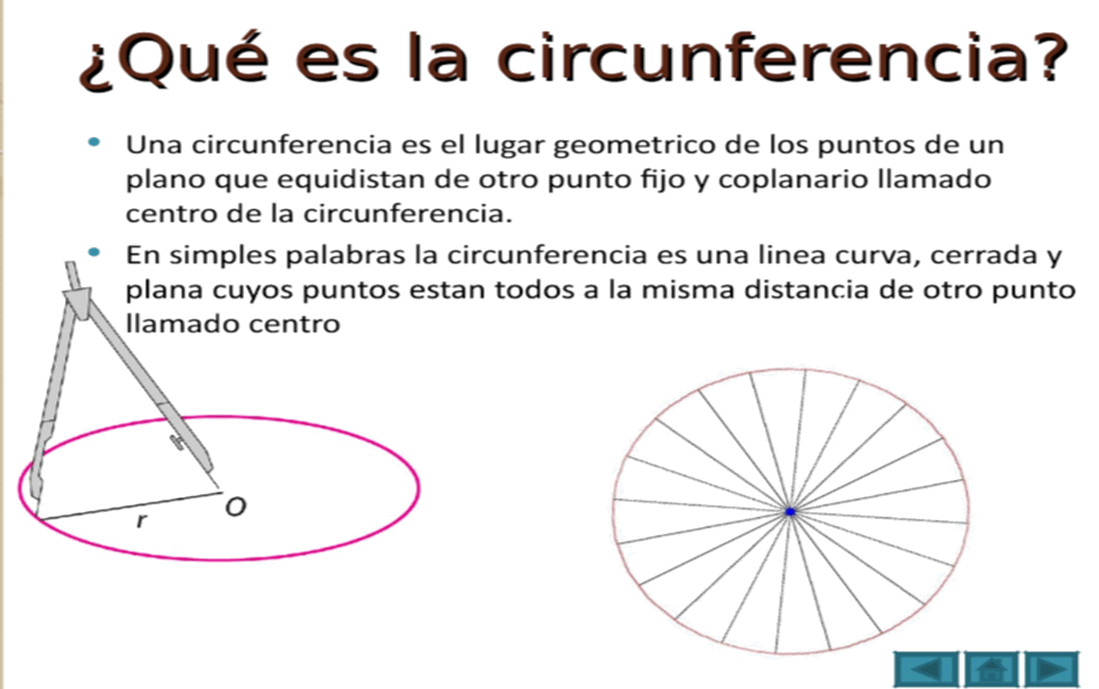
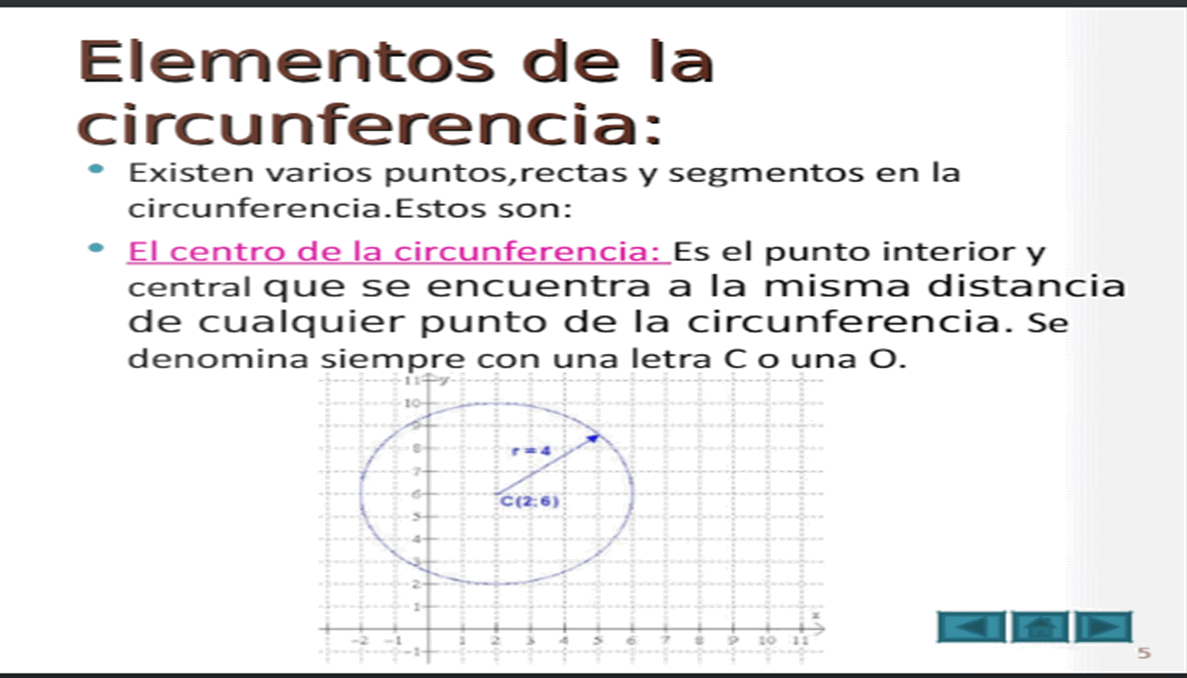
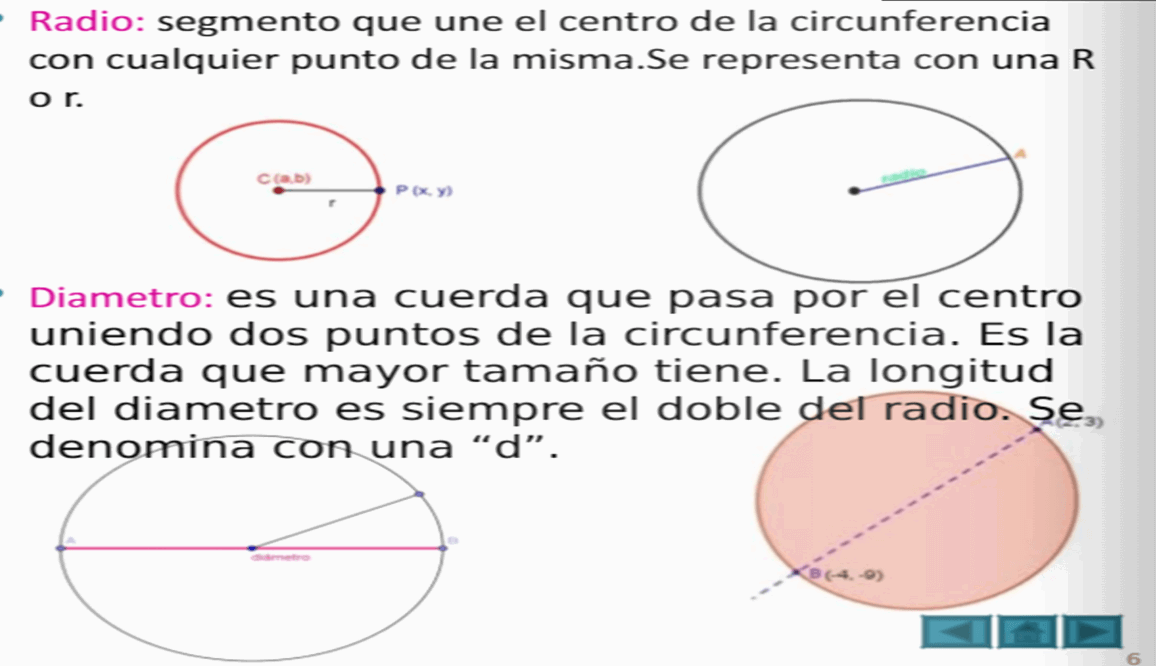
SEMANAS 17 Y 18

LÍMITE DE UNA FUNCIÓN

A finales de siglo XVIII y comienzos del XIX se inicio el desarrollo de la teoría de los límites para fundamentar el análisis matemático. Sin embargo, desde la antigüedad se aplicó el concepto de límite para resolver diversos problemas. 

1.1. IDEA INTUITIVA DE LÍMITE

Encontrar ellímite de una función f  significa hallar el valor al cual se aproxima f(x) cuando x  tiende a tomar un valor determinado.

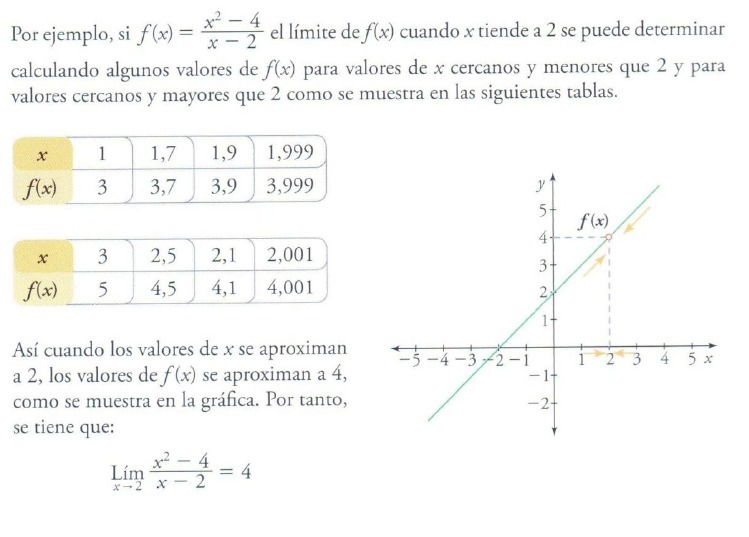
1.2. DEFINICIÓN FORMAL DE LÍMITE

La definición formal de límite se plantea de la siguiente forma:

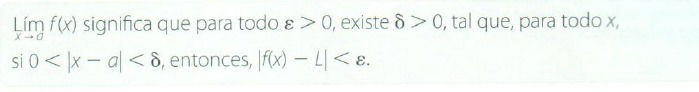
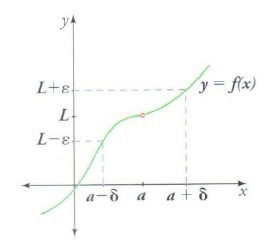
1.3. PROPIEDADES DE LOS LÍMITES

Hasta el momento se han determinado el límite de una función mediante tablas de valores o mediante la gráfica. Sin embargo, para facilitar el cálculo de límites es necesario aplicar sus propiedades.

SEMANAS 23 Y 24

LÍMITES LATERALES DE UNA FUNCIÓN

En algunas funciones como las definidas por partes y las de dominio restringido, como las que tienen raíces cuadradas, se aplican los límites laterales. Por ejemplo, en las funciones con radicales con índice par no tiene sentido hablar del límite en puntos a, extremos de los intervalos que conforman el dominio, pero los valores de la función se pueden acercar a un número cuando la variable se acerca por la derecha o por la izquierda al punto en cuestión. En las funciones definidas por intervalos servirán para establecer si la función tiene límite en los puntos donde la función cambia de fórmula y en caso que tenga límite en algún punto, determinar su valor.

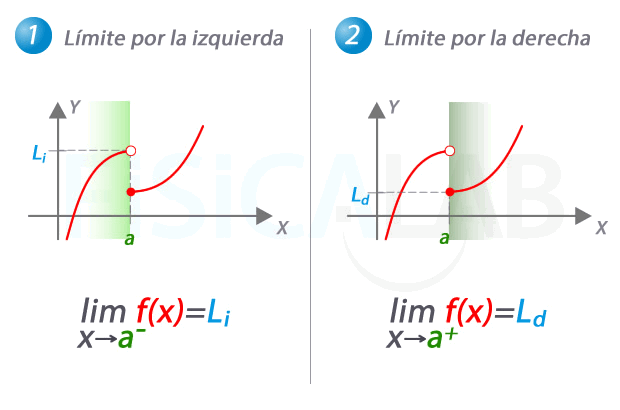
1. LÍMITE POR IZQUIERDA

El límite de f(x)  por la izquierda de a es L si la función  toma valores cada vez más próximos a L cuando x se aproxima al punto a por su izquierda.

Lo denotamos por

2. LÍMITE POR DERECHA

El límite de f(x)  por la derecha de a es L si la función  toma valores cada vez más próximos a L cuando x se aproxima al punto a por su derecha.

Lo denotamos por

GRÁFICAMENTE 

EJEMPLO

En las funciones definidas a trozos, es habitual que no coincidan los límites laterales en los puntos donde cambia la definición.

Por ejemplo, sea la función

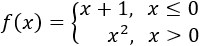
Los límites laterales en 0 son

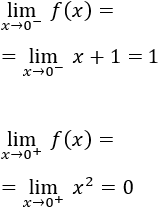
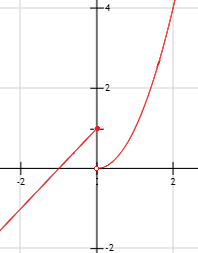
Gráfica:

CUARTO  PERIODO

SEMANAS 28 Y 29

  LÍMITES INDETERMINADOS

Los límites indeterminados (o indeterminaciones) no indican que el límite no exista, sino que no se puede anticipar el resultado.

Se tendrán que hacer operaciones adicionales para eliminar la indeterminación y averiguar entonces el valor del límite (en el caso de que exista). Ese valor puede ser un número finito, incluido el cero, o +∞ o bien -∞.

Aparecen indeterminaciones cuando, al sustituir la variable (x) de la expresión por el valor del límite al que tiende ésta, se convierte en uno de los casos siguientes:

Pero no serán indeterminaciones cuando, al realizar la sustitución mencionada de la variable por el valor de su límite, aparecen resultados como estos, siendo m un valor finito diferente de cero:

LA FORMA 0/0 

Este tipo de indeterminación, se suele presentar en cocientes de polinomios; cuando calculamos límites en un punto en el que se nos anula tanto el numerador como el denominador. Para resolver la indeterminación hay que descomponer en factores los polinomios, tanto del Numerador como del Denominador  y se genera el factor nulo en numerador y denominador, que al simplificarlo conduce a la resolución de la indeterminación.
En ocasiones, si esta indeterminación aparece asociada a raíces, binomios de raíces, se hace necesario multiplicar y dividir por el conjugado del binomio de raíces, para que aparezca el factor nulo.

 EJEMPLO:

Halle el siguiente limite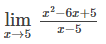 

Lo primero que se debe analizar al momento de resolver un límite es si presenta una indeterminación, para ello evaluamos  x, como se muestra a continuación. 

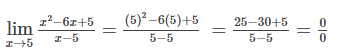
Se puede denotar del resultado anterior que el límite es indeterminado, por lo tanto se procede con métodos matemáticos para eliminar dicha indeterminación y encontrar su valor.

En el presente límite se denota que en el numerador se encuentra un trinomio, motivo por el cual se puede intentar una factorización. 

x²−6x+5

Para lograr factorizar el trinomio anterior se deben encontrar dos números que multiplicados den 5 y sumados -6.

Los números que cumplen con esa condición son -5 y -1.

La expresión queda representada de la siguiente manera:

x²−6x+5 = (x−5)(x−1)

Luego de realizar la respectiva factorizacion se procede a eliminar la indeterminación.

LÍMITE INFINITO MENOS INFINITO

Por tanto, para calcular el límite, tenemos que fijarnos en el orden de los infinitos. En el límite de un polinomio, la resta de infinitos es el infinito de mayor orden (el infinito que corresponde al monomio de grado mayor es el de mayor orden).

Esto implica que, además, el signo del resultado depende del coeficiente del monomio de grado mayor. Por ejemplo,

Cuando x tiende a infinito negativo, es un poco más complicado. En este caso, lo más sencillo es sustituir, calcular los signos (depende de la paridad de las potencias) y comparar el orden de cada infinito.

Por ejemplo,

El resultado es infinito positivo porque el signo del infinito de mayor orden es positivo.

 SEMANAS 33 Y 34 (Corte 3)

Indeterminación división entre infinitos