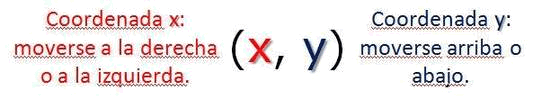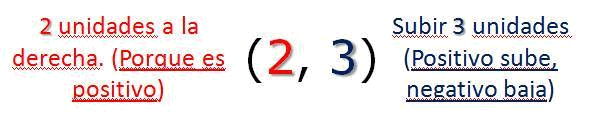GEOMETRÍA - SÉPTIMO
SEMANA 11
ÁREAS Y PERÍMETROS
Teniendo en cuenta la investigación realizada en el cuarto corte del primer periodo haremos un pequeño repaso en cuanto al área y perímetro de los polígonos.
ÁREA
El área de una figura es la medida de superficie que ocupa la figura. El área se simboliza con la letra A.
Para determinar el área de una figura se elige una cantidad cuadrada y se cuenta la cantidad de estas unidades necesarias para recubrir la figura. Este procedimiento se llama recubrimiento,
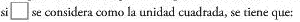
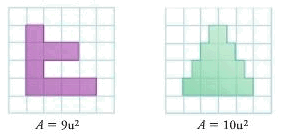
- Unidades métricas de área
La unidad fundamental de área es el metro cuadrado y se simboliza por m2 , que corresponde a la medida de la superficie de un cuadrado cuyo lado mide 1 m.
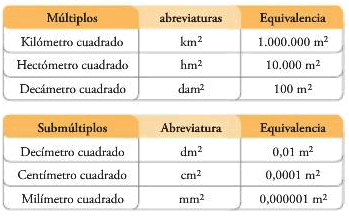
El metro cuadrado tiene unidades de orden superior llamados múltiplos y unidades de orden inferior llamados submúltiplos.
PERÍMETRO
El perímetro de una figura plana es igual a la suma de las longitudes de sus lados.
Ejemplo
Supongamos que las medidas de los lados de este polígono son a = 2 cm, b = 4 cm, c = 3 cm y d = 1 cm; entonces, su perímetro será:
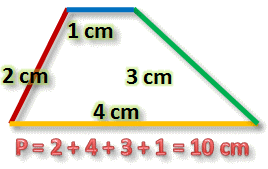Tomado: http://www.bartolomecossio.com/MATEMATICAS/permetro_de_un_polgono.html
SEMANA 12
CONVERSIONES DE UNIDADES DE ÁREA
Los múltiplos y los submúltiplos del metro cuadrado pueden expresarse como potencias de 10, con lo cual es posible realizar la conversión de una unidad de medida de área a otra.
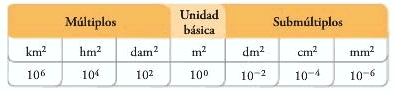
Cada potencia de 10 se expresa en metros cuadrados y cada unidad de área es 100 veces mayor que la inmediatamente inferior y 100 veces menor que la inmediatamente superior. Así, para determinar la equivalencia de una unidad de orden superior a una unidad de orden inferior se multiplica por 100, 10.000, 1.000.000, etc.
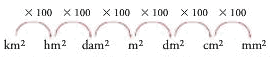
Para hallar la equivalencia de una unidad de orden inferior a una unidad de orden superior, se divide entre 100, 10.000, 1.000.000, etc.
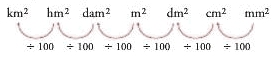
EJEMPLO:
Convertir a la unidad indicada.
- 18,124 dam2 a m2.
Al realizar la conversión de la unidad de la unidad de orden superior dam2 a la unidad de orden inferior m2 , se debe multiplicar por 100, pues hay un lugar entre dam2 y m2 . Luego la equivalencia de 18,124 dam2 a m2 es:
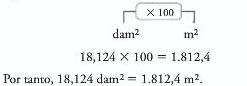
SEMANA 14
PLANO CARTESIANO
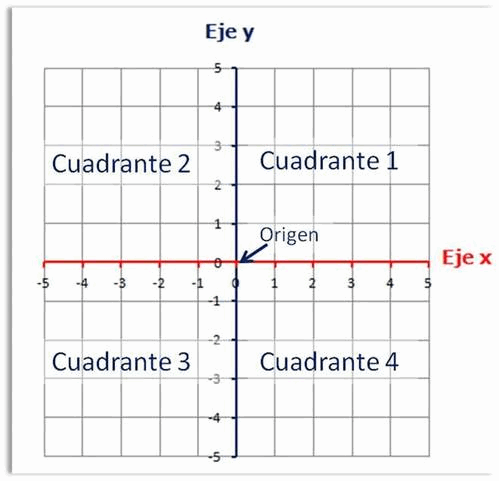
Plano cartesiano. Es la unión de dos rectas perpendiculares que dividen un plano en cuatro cuadrantes. A la recta horizontal se le llama eje de las ”x”, o, abscisas y a la recta vertical se llama eje de las “y” u ordenadas. Formando de esta manera cuatro cuadrantes.
El plano cartesiano debe su nombre al filósofo francés René Descartes (1596-1650), creador del campo de la geometría analítica.
Cada punto en el plano cartesiano puede representarse con un par ordenado de números (x, y).
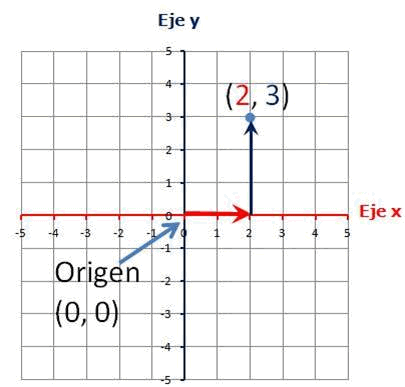
Para trazar un punto de un par ordenado, parte del origen, el punto (0, 0), donde se cruza el eje de las x y el eje de las y. La primera coordenada indica las unidades que hay que desplazarse en x, a la izquierda o a la derecha; la segunda indica cuántas unidades hay que subir o bajar.
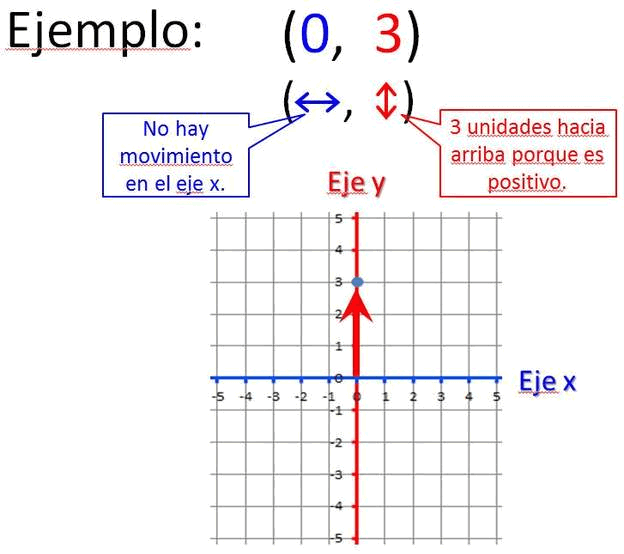
Ejemplo 1:
SEMANAS 21 Y 22
HALLAR LAS COORDENADAS EN EL PLANO
Anteriormente hemos estudiado el plano cartesiano, sus elementos y como ubicar puntos conociendo sus correspondientes coordenadas.
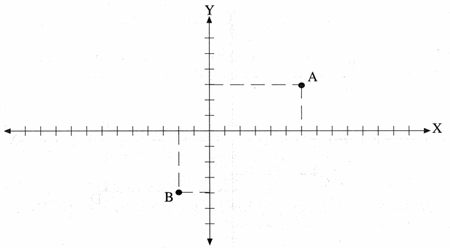
En ocasiones es necesario identificar las coordenadas de un punto observando su localización con respecto al origen. Por ejemplo:
El punto A se localiza en la intersección de las perpendiculares del eje de las abscisas en el punto 6 y del eje de las ordenadas en el 3; por lo tanto, sus coordenadas son (6, 3).
El punto B se localiza en la intersección de las perpendiculares del eje de las abscisas en el punto -2 y del eje de las ordenadas en el -4, por lo tanto, sus coordenadas son (-2, -4).
En el plano cartesiano es posible representar expresiones algebraicas y su uso abarca no sólo aspectos estrictamente matemáticos sino también relativos a otras ramas de la ciencia.
Posteriormente se contabilizan las unidades en el EJE DE LAS ABSCISAS y en el EJE DE LAS ORDENADAS obteniendo las coordenadas del punto en cuestión.
Para dar la ubicación del punto se dicta primero las unidades del EJE X y después las del EJE Y. (x,y)
Que en este caso, sería (-3, 1).
SEMANAS 23 Y 24
TRASLACIONES DE FIGURAS EN EL PLANO
La traslación es una transformación que consiste en desplazar una figura a lo largo de una línea recta conservando la longitud de sus lados y la medida de sus ángulos.
Para determinar la traslación de una figura es necesario indicar los tres elementos de una traslación:
- La dirección, que puede ser horizontal o vertical.
- El sentido, que puede ser derecha, izquierda, arriba o abajo.
- La magnitud, que corresponde al número de unidades que se va a trasladar la figura.
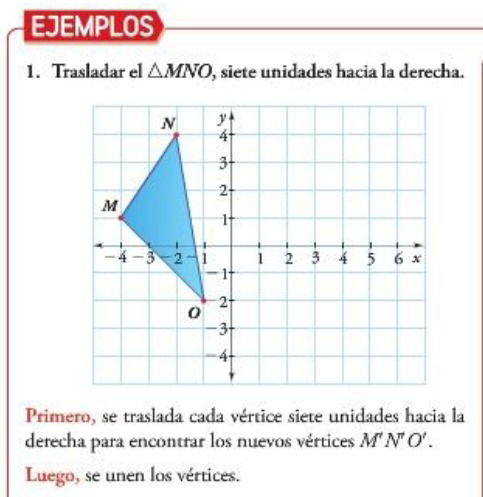
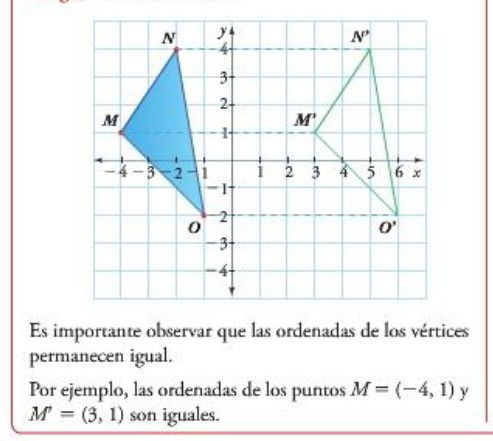
La figura anterior se ha trasladado:
- En dirección horizontal.
- Con sentido hacia la derecha.
- Magnitud de siete unidades
