GEOMETRÍA - OCTAVO

SEMANA 11
CONGRUENCIA DE TRIÁNGULOS
A partir de la investigación hecha en el cuarto corte del primer periodo sobre congruencia de triángulos haremos algunos ejemplos para entender mejor la temática y revisaremos otros criterios especiales.
CRITERIOS DE CONGRUENCIA DE TRIÁNGULOS

Los criterios anteriormente expuestos son los mas comunes y utilizados para demostrar la congruencia de triángulos , pero existen otros criterios especiales que se usan para ciertos triángulos en particular en los triángulos rectángulos.
Estos criterios son :
CRITERIO DE CONGRUENCIA CATETO - CATETO
Dos triángulos rectángulos son congruentes si los catetos de uno de los triángulos tienen la misma medida que los catetos correspondientes del otro.
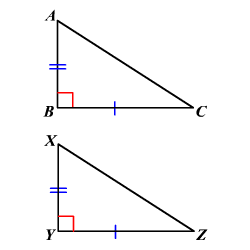
En la figura, 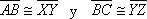 .
.
Así 
CRITERIO DE CONGRUENCIA CATETO - ÁNGULO
Dos triángulos rectángulos son iguales cuando tienen, respectivamente iguales un cateto y un ángulo agudo.
En la figura, 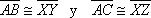 .
.
Así, 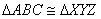 .
.
CRITERIO DE CONGRUENCIA HIPOTENUSA - CATETO
Dos triángulos rectángulos son iguales cuando tienen iguales la hipotenusa y uno de los catetos.

En la figura, 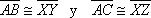 .
.
Así, 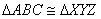 .
.
CRITERIO DE CONGRUENCIA HIPOTENUSA - ÁNGULO
Dos triángulos rectángulos son iguales cuando tienen respectivamente iguales la hipotenusa y un ángulo agudo.
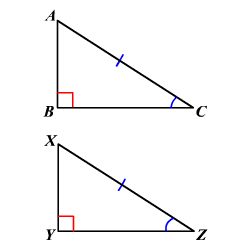
En la figura, 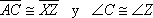 .
.
Así, 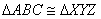 .
.
SEMANA 11
CONGRUENCIA DE TRIÁNGULOS
SEMANAS 19 Y 20
ÁREA DE LOS POLIEDROS
Anteriormente estudiamos las áreas de las figuras planas. En este tema nos dedicaremos a estudiar las superficies que envuelven a los cuerpos geométricos o cuerpos sólidos.
Entendemos por cuerpo sólido al que ocupa un lugar en el espacio. Es decir, el que contiene las tres dimensiones (largo, ancho y alto).
Los poliedros regulares tiene todos sus ángulos diedros y todos sus ángulos poliedros iguales y sus caras son polígonos regulares iguales.
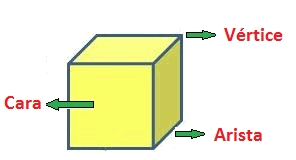
Tipos de poliedros regulares
Sólo existen cinco poliedros regulares:
- Tetraedro
- Hexaedro o cubo
- Octaedro
- Dodecaedro
- Icosaedro
Tetraedro
Un tetraedro es un poliedro regular que tiene 4 caras que son triángulos equiláteros.
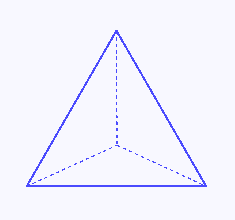
Área del tetraedro

Recuerde que para hallar el área total de un tetraedro se usa la formula anterior, pero también puede hallarla mediante el Área de una de sus caras (triángulo) y multiplicar el resultado por 4 (# de caras).
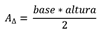
Y el área total del poliedro sera:
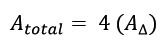
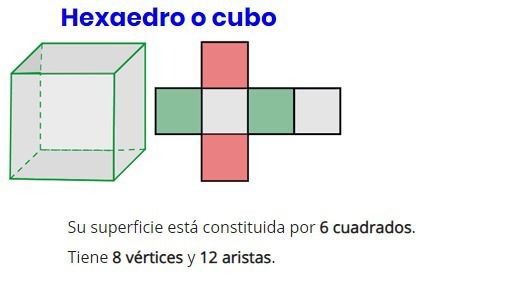
Área total del hexaedro regular o cubo
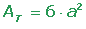
SEMANAS 20 Y 21
ÁREA DE LOS POLIEDROS
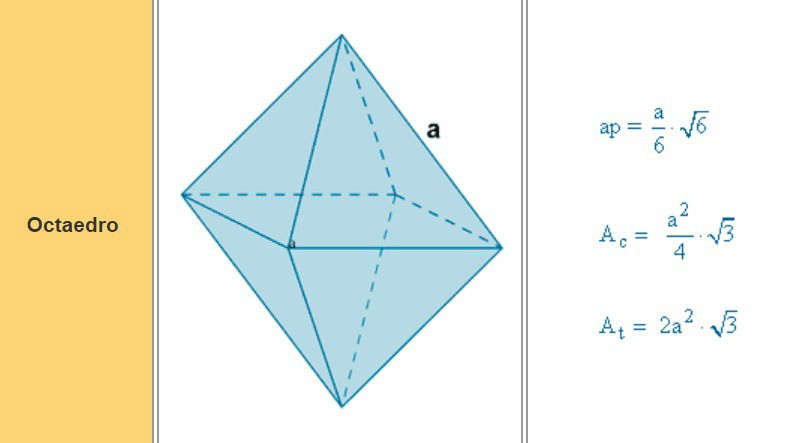
OCTAEDROS
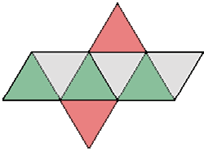
Su superficie consta de ocho triángulos equiláteros.
Tiene 6 vértices y 12 aristas.
Se puede considerar formado por la unión, desde sus bases, de dos pirámides cuadrangulares regulares iguales.
En clase se estableció que se puede hallar el área toral de igual forma que el tetraedro cuando se usa el área de una de sus caras, pero teniendo en cuenta que ahora multiplicaremos por ocho caras.
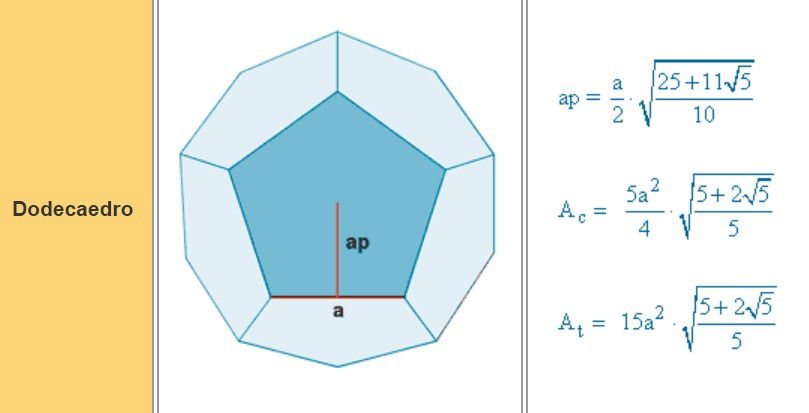
DODECAEDROS
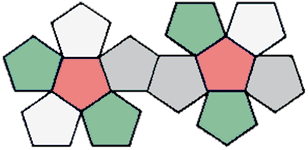
Su superficie consta de 12 pentágonos regulares.
Tiene 20 vértices y 30 aristas.
En clase se estableció una ecuación para la apotema aunque se expone otra forma de hallarla para que tomen la que mejor les convenga.
ICOSAEDROS
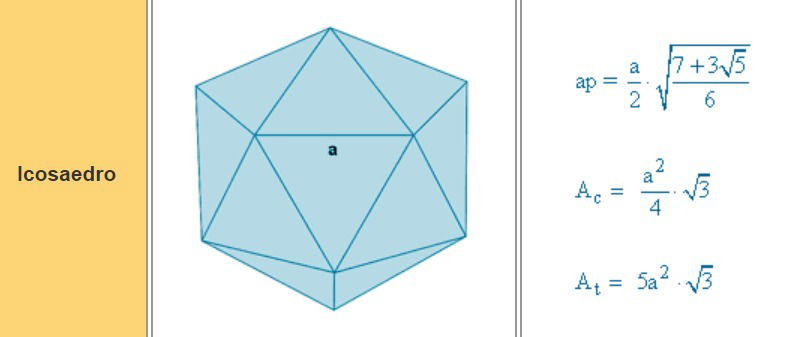
Su superficie consta de veinte triángulos equiláteros.
Tiene 12 vértices y 30 aristas.
SEMANAS 23 Y 24
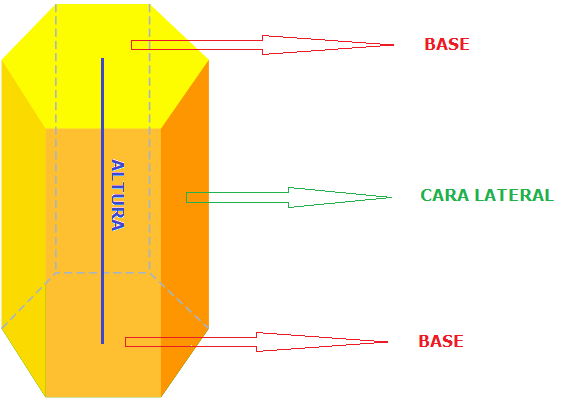
LOS PRISMAS
Un prisma es un poliedro cuya superficie está formada por dos caras iguales y paralelas llamadas bases y por caras laterales (tantas como lados tienen las bases) que son paralelogramos.
ELEMENTOS PRINCIPALES DE UN PRISMA
- Bases: Todos tienen dos bases, siendo ambas iguales y paralelas.
- Caras laterales: Son los paralelogramos comprendidos entre las 2 bases.
- Altura: Es la distancia entre las dos bases.
CLASIFICACIÓN DE LOS PRISMAS
Los prismas se pueden clasificar dependiendo 4 características que lo definen. Estas características o criterios son:
1. NÚMERO DE LADOS DE LA BASE
Los primas se pueden clasificar según el número de lados que tienen sus bases
- Prisma triangular: las bases son triángulos (3 lados).
- Prisma cuadrangular: las bases son cuadriláteros (4 lados).
- Prisma pentagonal: las bases son pentágonos (5 lados).
- Prisma hexagonal: las bases son hexágonos (6 lados)
- y así sucesivamente…

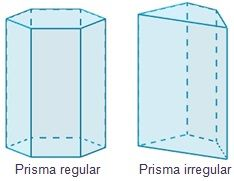
2. REGULAR O IRREGULAR
- Prisma regular: un prisma es regular si sus bases son polígonos regulares
- Prisma irregular: los prismas son irregulares si tienen polígonos irregulares en su base.
3. RECTO U OBLICUO
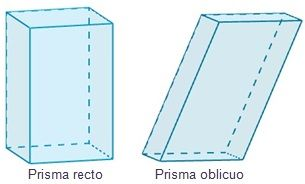
- Prisma recto: si los ejes de los polígonos de las bases son perpendiculares a las bases. Las caras laterales son cuadrados o rectángulos.
- Prisma oblicuo: es aquel cuyos ejes de los polígonos de las bases se unen por una recta oblicua a las bases mismas.
4. CONVEXO O CÓNCAVO
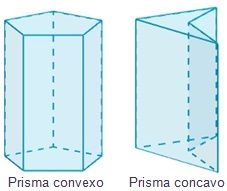
- Prisma convexo: el prisma es convexo si sus bases son polígonos convexos.
- Prisma cóncavo: el prisma cóncavo tiene como bases dos polígonos cóncavos iguales.
CUARTO PERIODO
SEMANAS 28 Y 29
ÁREA DE LOS PRISMAS
En las siguiente presentación se muestran los conceptos vistos en clase


